Map

Definition

Stores a collection of key-value pairs (unique keys, no such restriction on values)

Also known as: dictionary, associative array

Main operations

• addPair and removePair (based off key)
• valueLookup

Implementations

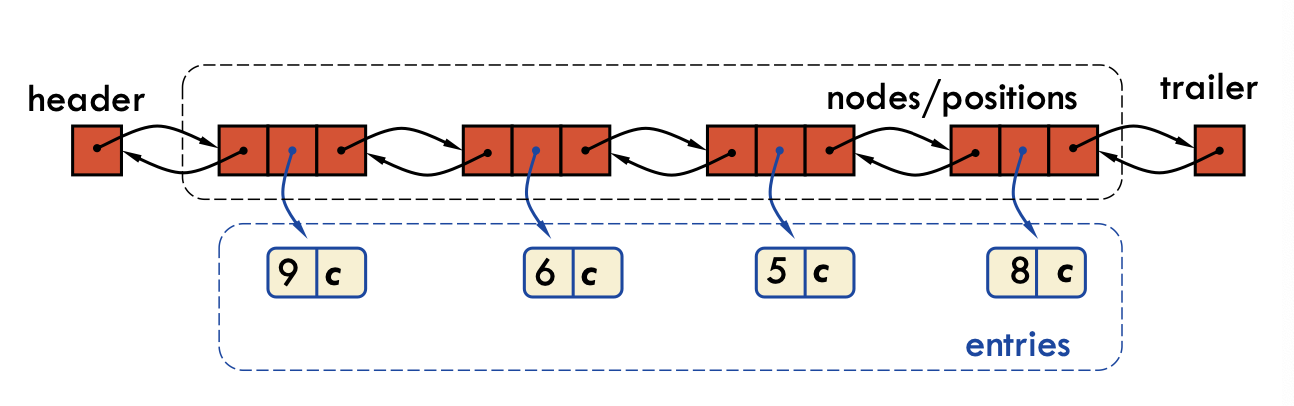
Naive list

Using an unsorted list, we can use a List ADT related data structure (e.g.: Doubly-linked list) to store the entries

Performance

• get(), removePair() will be worst-case $O(n)$ as we need to traverse the entire sequence to look for the pair with that key

Evaluation

Only really suitable where searches and removals are highly uncommon and we mostly have addPair() operations where we know the key is new, as we can add $O(1)$ entries to the end of the list

Arrays with restricted keys

Use an Array of size $N$ where the index acts as the key

Performance

• $O(1)$ for all operations due to direct access in Array

Evaluation

• Great worst-case time complexity
• However, unable to handle general keys (e.g.: strings)
• Bad space utilisation esp. when the key set is sparse compared to possible keys, costly to resize

Hash map

Main article: Hash table

Binary search tree

Implementation	Time Complexity	Space Complexity	Advantages	Disadvantages
Array-based (naive)	Insert: O(n) Delete: O(n) Search: O(n)	O(n)	Simple and straightforward	Not efficient for large maps
Linked list-based	Insert: O(1) Delete: O(1) Search: O(n)	O(n)	Efficient for large maps Easy to implement	Slower than hash table or binary search tree for search operations
Binary search tree-based	Insert: O(log n) Delete: O(log n) Search: O(log n)	O(n)	Efficient for large maps Sorted keys	Worst case time complexity can be O(n) if the tree is unbalanced
Hash table-based	Insert: O(1) Delete: O(1) Search: O(1)	O(n)	Very efficient for large maps Constant-time operations on average	Hash collisions must be handled Resizing can be expensive

---

• task Add BST Map implementation details