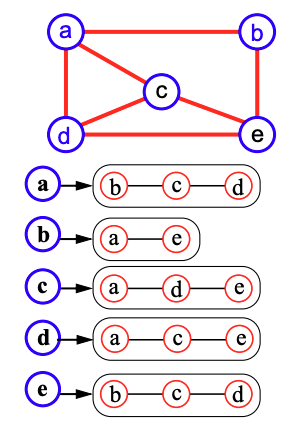
Basic adjacency list graph data structure

Basic adjacency list graph data structure

Each vertex stores its own sequence of vertices it is adjacent to

USYD content

This is not the adjacency list covered at The University of Sydney. Refer to: “Modern” adjacency list with incidence containers

Time complexities

Where $n$ is the # of vertices, $m$ is the # of edges

Operation	Complexity	Notes
Space	$O(n+{\sum }_{deg(v)})\le O(n+m)$	n elements for each vertex, then at most 2m elements for each endpoint of the m vertices
insertVertex(x)	$O(1)$	Add a new vertex list
insertEdge(u,v,x)	$O(1)$	Add adjacent vertex element to 2 places
removeVertex(v)	$O(n+m)$	Remove the vertex from the adjacency list and also remove all edges connected to that vertex
removeEdge(e)	$O(m)$	Search for and remove the edge from both vertices’ adjacency lists
degree(v)	$O(1)$	Track size of vertex’s adjacency list
incidentEdges(v)	$O(deg(v))$	Traverse adjacency list
get/isEdge(u,v)	$O(min(deg(u),deg(v)))$	Get degree of the 2 vertices, traverse adjacency list of smaller to check existence of edge
endVerticesOf(e)	N/A
opposite(v,e)	N/A
vertices()	$O(n)$	Traverse V
edges()	$O(m)$	Traverse all the adjacency lists - O(2m) reduces
numVertices()	$O(1)$	Dependent on a counter variable
numEdges()	$O(1)$	Dependent on a counter variable

The above time complexities are not double-checked