Edge list graph data structure

Store two unsorted lists

• A vertex sequence with a list of vertices
• An edge sequence with a list of vertex pairs

Where $n$ is the # of vertices, $m$ is the # of edges

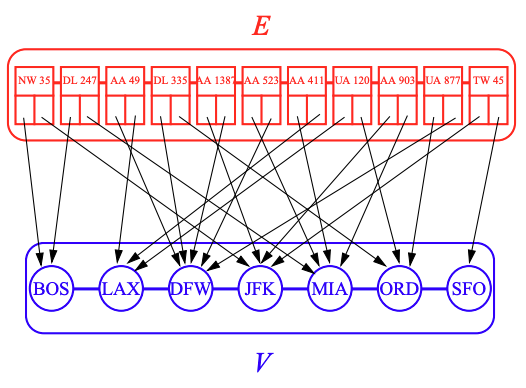
Use a doubly linked list as the container for $V$ and $E$ for optimal time complexity

Using an array is easier but things like removeEdge will become $O(n)$ due to increased deletion time complexity

Time complexities

Where $n$ is the # of vertices, $m$ is the # of edges

Operation	Complexity	Notes
Space	$O(n+m)$	Two lists
insertVertex(x)	$O(1)$	Add to V sequence
insertEdge(u,v,x)	$O(1)$	Add to E sequence
removeVertex(v)	$O(m)$	Need to traverse edges to remove incident edges
removeEdge(e)	$O(1)$	Remove from sequence - given doubly-LL
degree(v)	$O(m)$	Traverse all edges to count
incidentEdges(v)	$O(m)$	Traverse all edges to return incident one
getEdge(u,v)	$O(m)$	Traverse all edges to return pointer to matching pair
endVerticesOf(e)	$O(1)$	Edge pointer given - return the relevant vertex pointers
opposite(v,e)	$O(1)$	Edge pointer given - return other vertex
vertices()	$O(n)$	Traverse V
edges()	$O(m)$	Traverse E
numVertices()	$O(1)$	Dependent on a counter variable
numEdges()	$O(1)$	Dependent on a counter variable

• Can be implemented as a pair of Doubly-linked list where the $E$ nodes store two pointers to the connected vertices
• Array can also be used - the $E$ array can store tuples of vertex pointers. Worse time complexity

Directed graph information

See this link